Diffeomorphic Flow Matching
Using a vectorfield learned by Flow Matching to transform given contractive dynamics
Goal: Learn a contractive policy conditioned on the given scene
Idea: Transform a given base contractive dynamical system leveraging image embeddings and flow matching policies. Use the generated vectorfield as a diffeomorphism to map the base dynamics in to the target system beeing contractive towards the target trajectory.
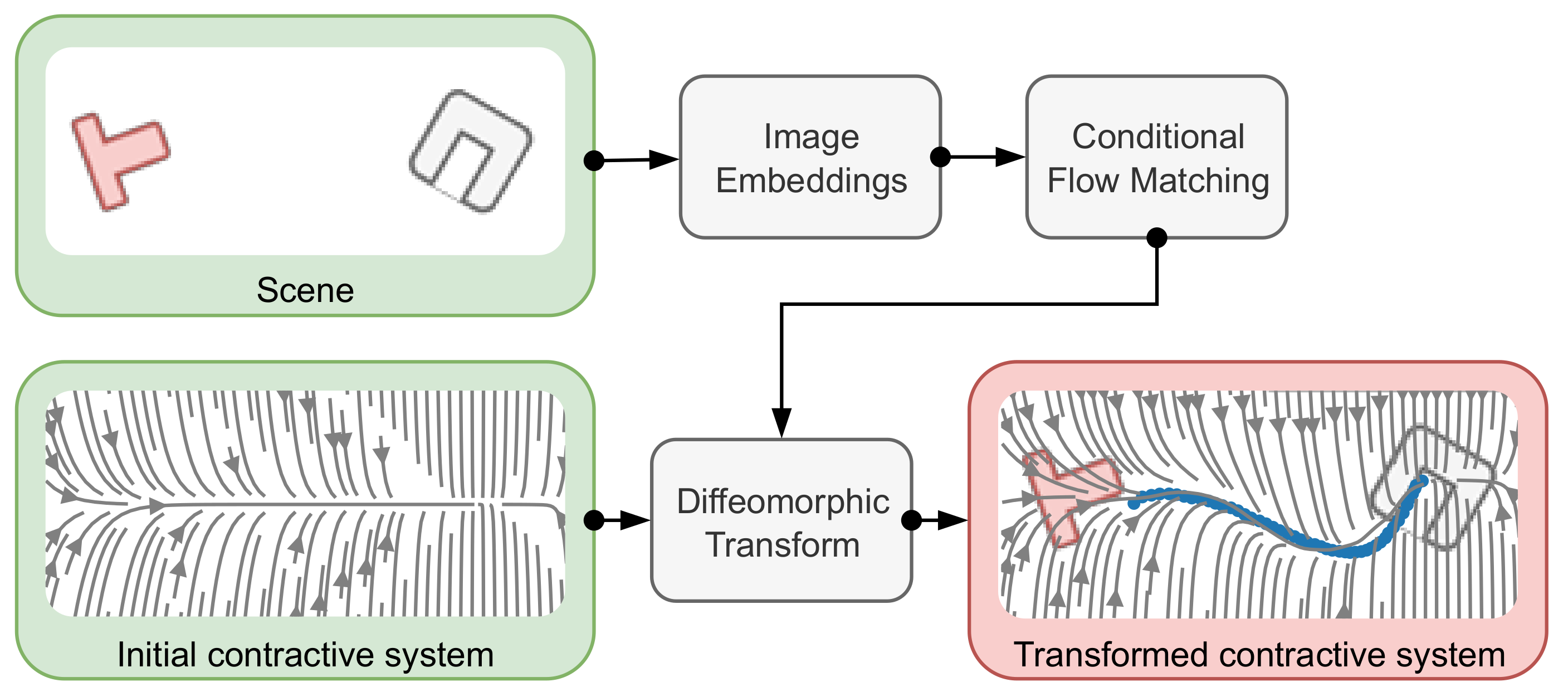
To extract the image embeddings, DINOv2 with Registers is used. Given these embeddings a conditioned Unet backbone is trained using Flow Matching. The model architecture is analogous to Diffusion Policy. Given this learned flow \(𝑉_\text{FM}\) defines a infinitesimal generator, which again defines a diffeomorphism \(\psi_\text{DT}\) over a flow \(\gamma\).
\[\psi_\text{DT}(\mathbf{x}) = \mathbf{x} + \int 𝑉_\text{FM} (\gamma(\mathbf{x}, u))\]Given this diffeomorphic transform, I transform the base contractive dynamics \(f_\text{c}\) into the target dynamical system \(f_\text{target}\), as follows
\[f_\text{target}(\mathbf{x}) = \mathbf{J}_{\psi_\text{DT}}^{-1}(\mathbf{x})f_\text{c}(\psi_\text{DT}(\mathbf{x}))\]This approach is inspired by the paper Euclideanizing Flows.
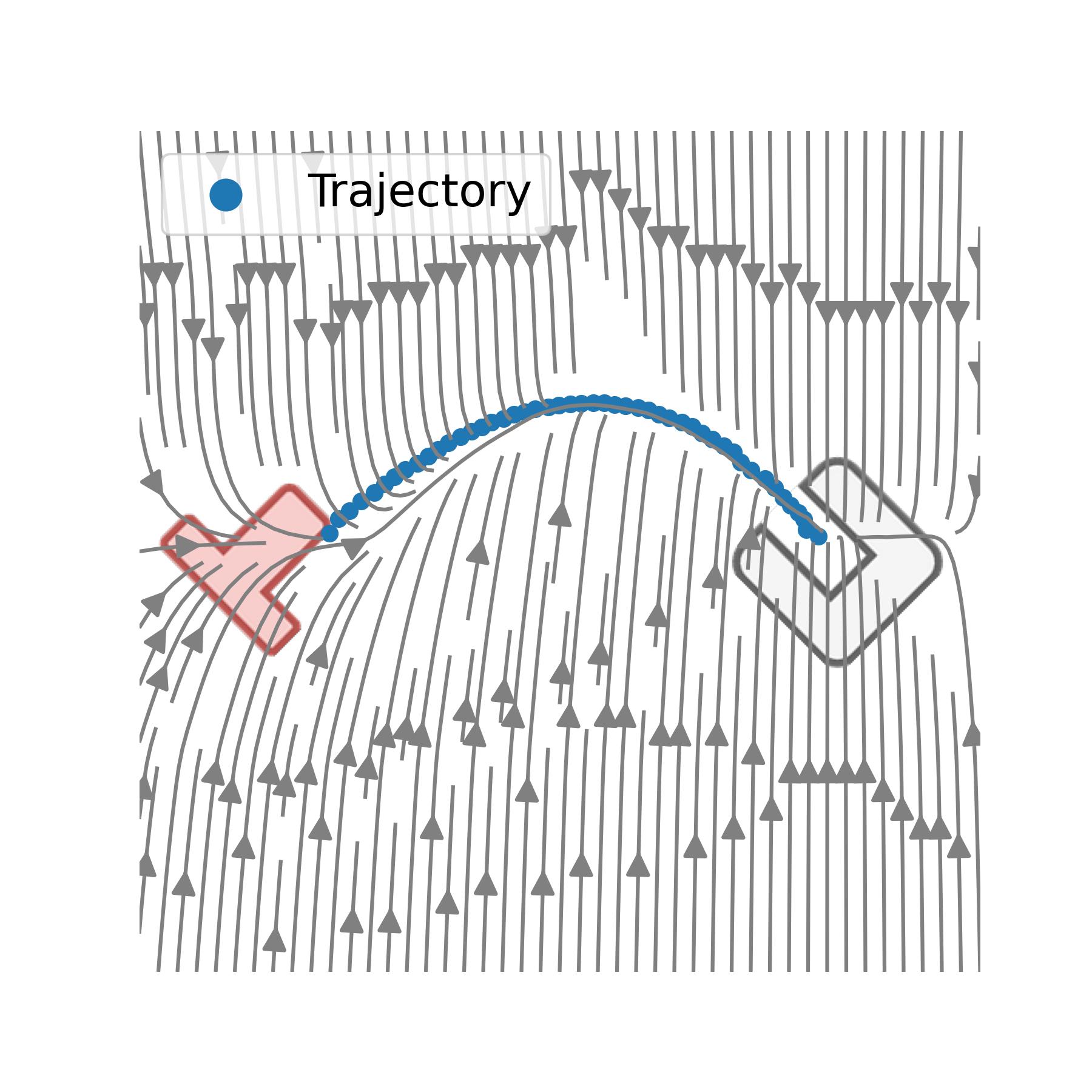
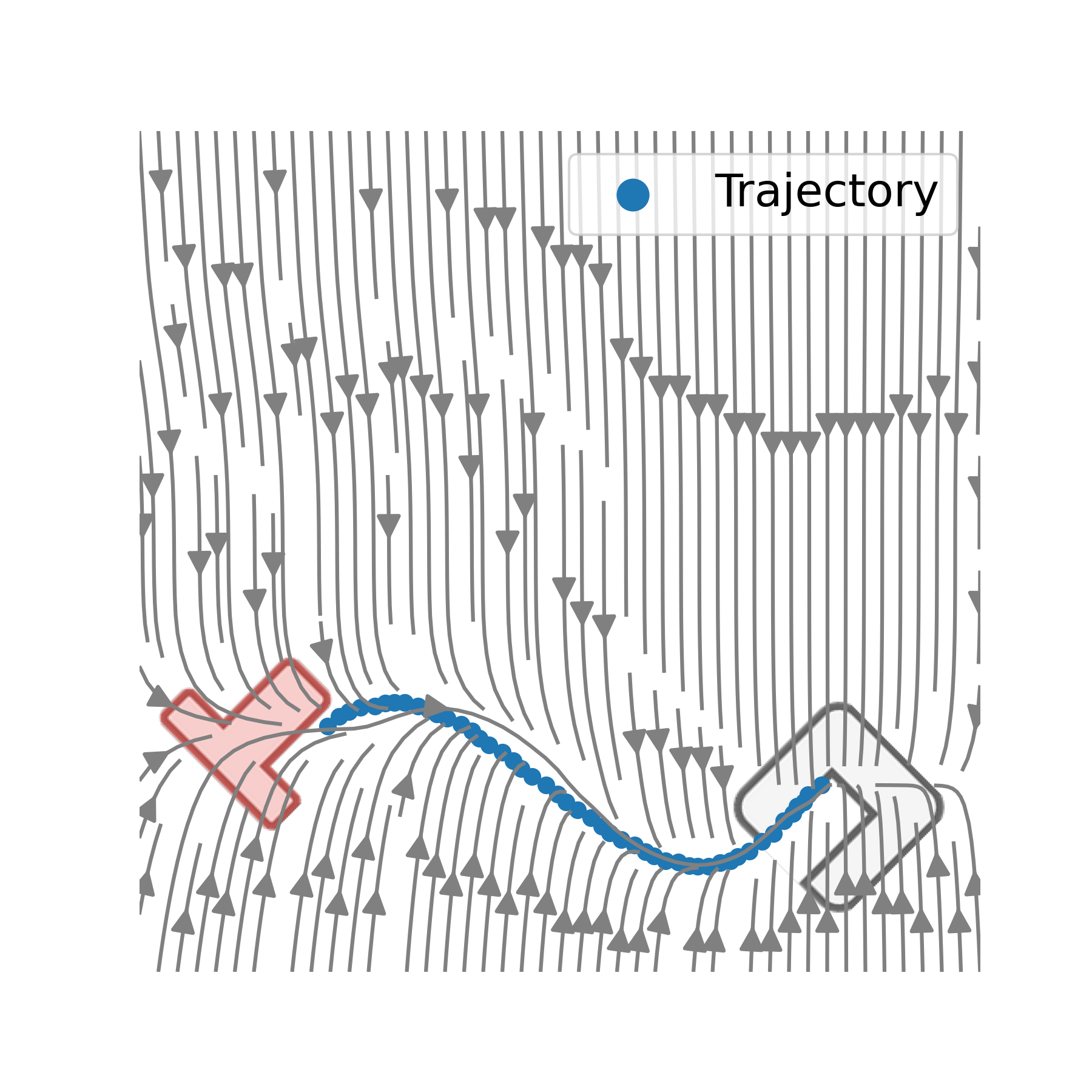
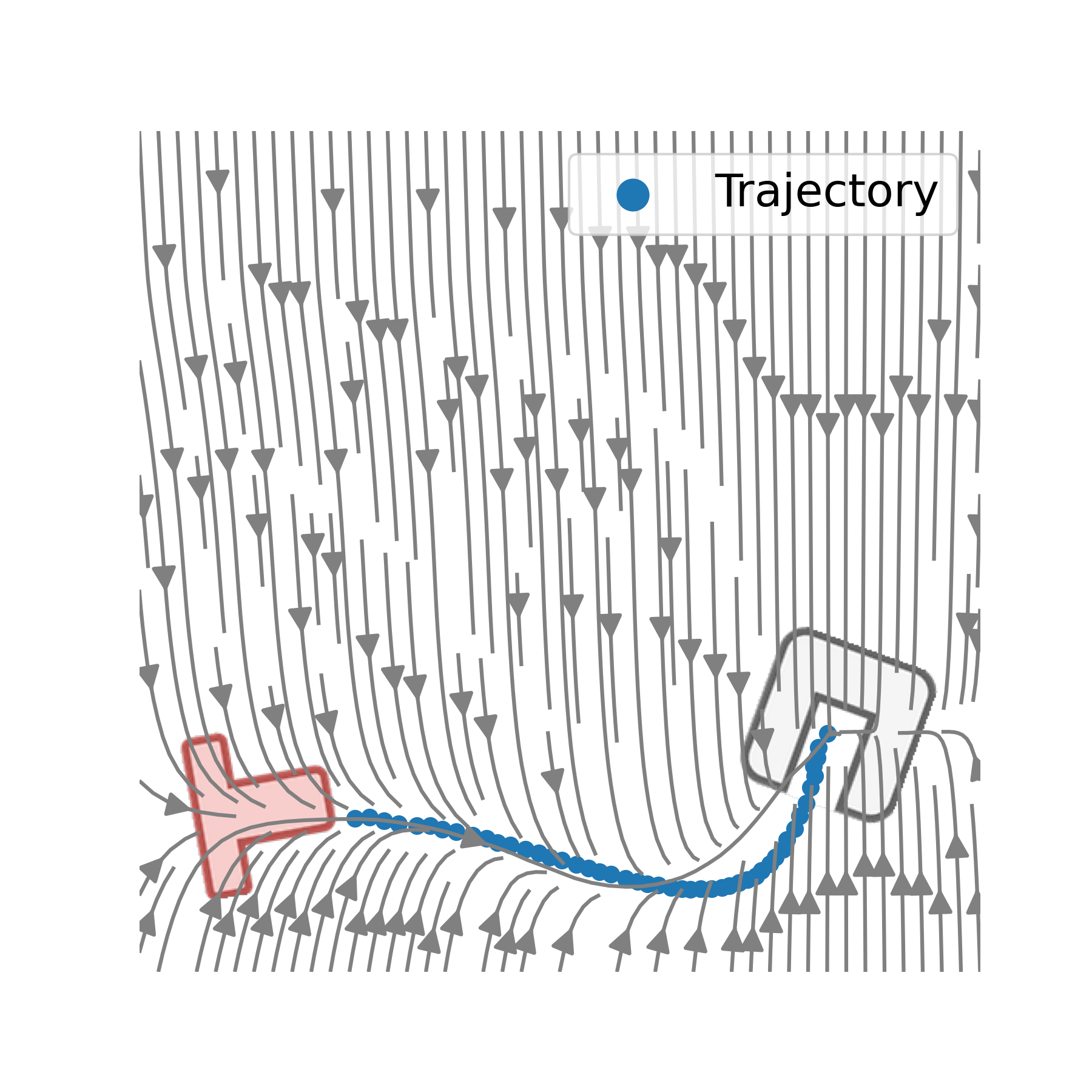
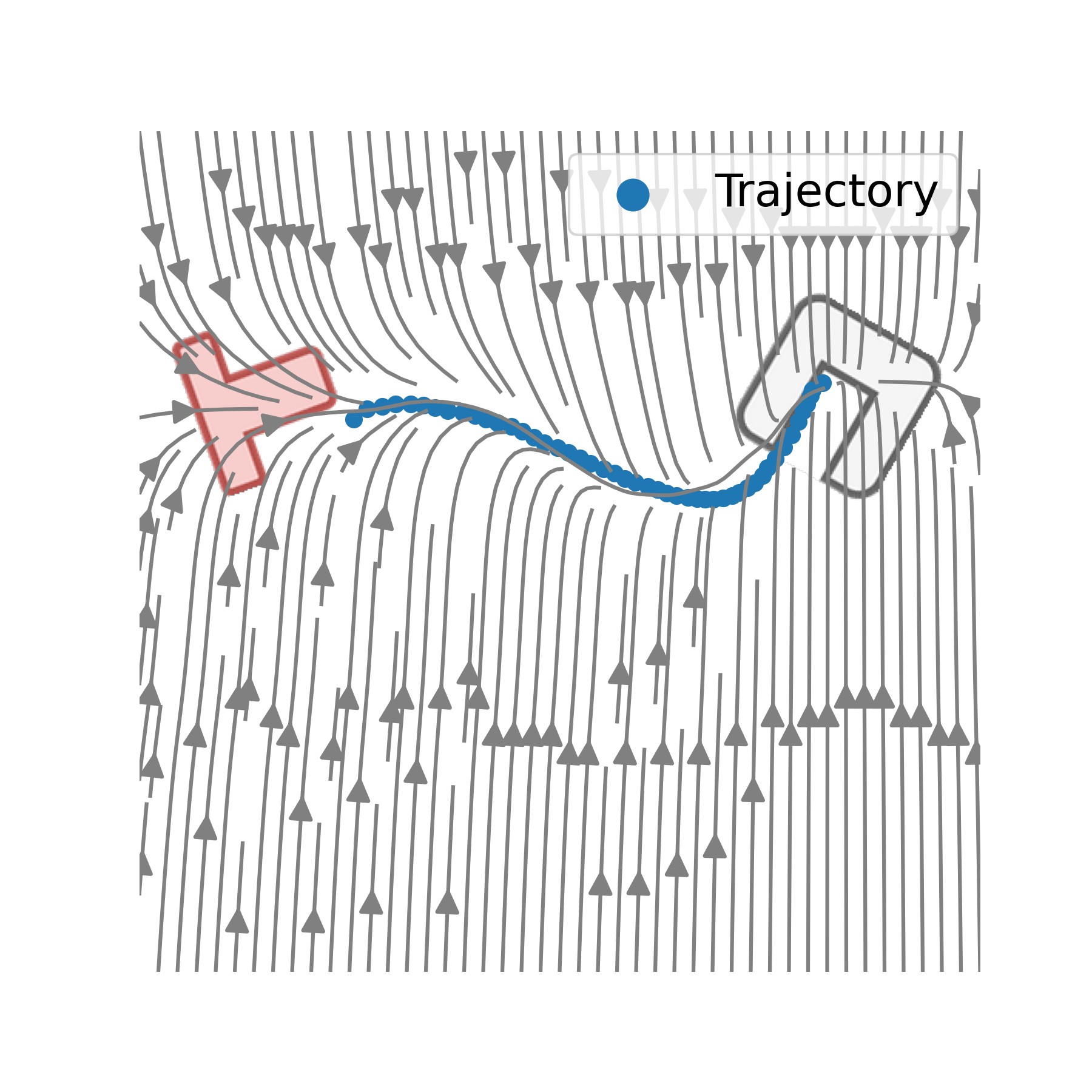
Experiments: Move a T-Profile stable into an U-Profile.
Just the picture of the scene is given. For training a spline trajectory between both profiles are calculated as groundtruth. 5000 scene and trajectory pairs a generated and sampled from a normal distribution. The final MSE on test dataset is \(0.297\) and on traing dataset: \(0,023\) (just the generated trajectories).
